椭圆与圆的关系
圆是一个很简单很对称的图形,它是平面中到圆心的距离为定值的所有点组成的图形。椭圆是对圆定义的一个扩展,它是平面中到两个点的距离之和为定值的所有点组成的图形,这两个点被称为焦点、两个点之间的距离称为焦距。当两个焦点重合时,椭圆也就变成了圆。
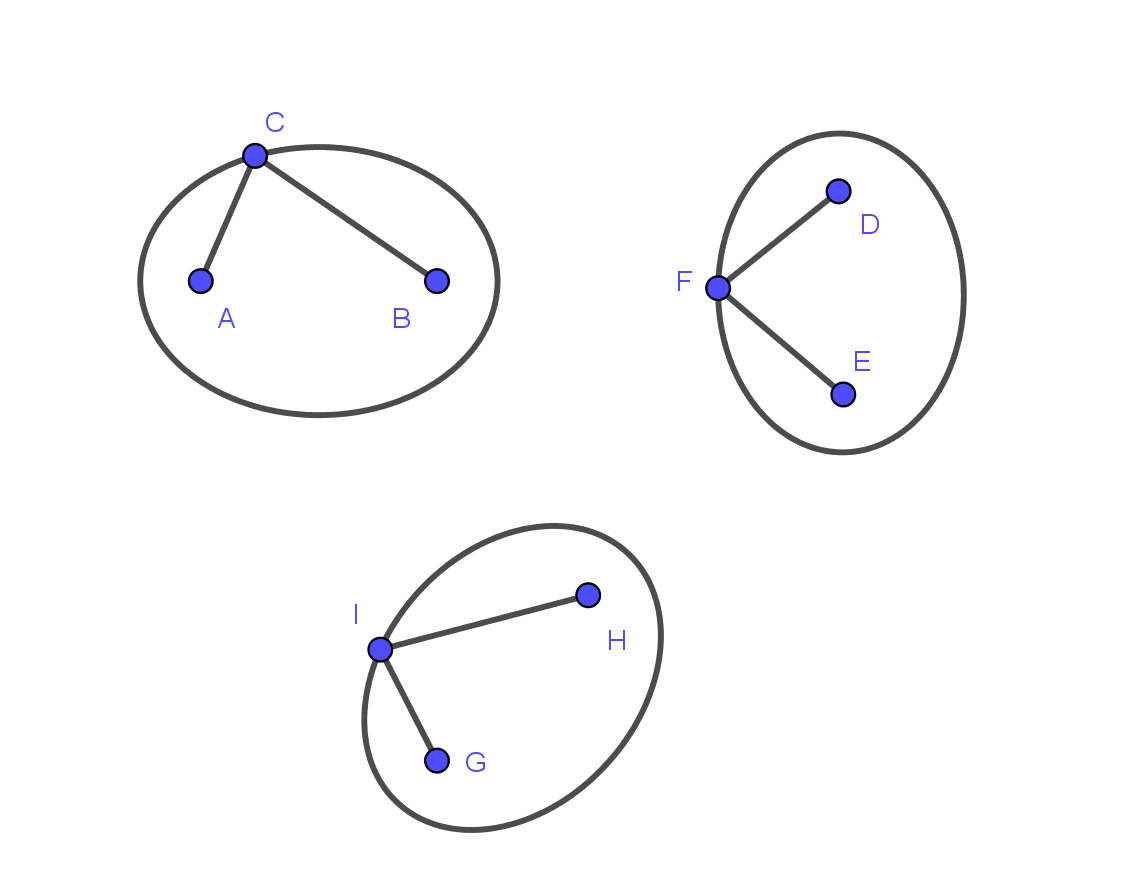
假设有一条绳子,它的两个端点是固定的,绳子长度超过两个固定点的距离,拿一枝笔将绳子拉直,用这支笔绕一周画出来的图形轨迹就是椭圆,两个固定端点就是椭圆的焦点。
椭圆的形状、方向
椭圆是一个平面图形,对于平面图形我们通常会想办法建立坐标系来进行表示。椭圆定义中没有指定两个焦点的位置和方向,因此椭圆的大小、位置和方向都是可以变化的。由于椭圆是一个对称的图形,同时满足轴对称和中心对称,因此,为了简单起见,通常选取原点作为椭圆的对称中心,两个坐标轴作为椭圆的对称轴,那么此时椭圆焦点应该是坐标轴上两个对称的点。
给定以上条件之后,椭圆方程的求解就不难了。下面我会给出焦点在x轴上的椭圆方程的推导。
椭圆方程的推导
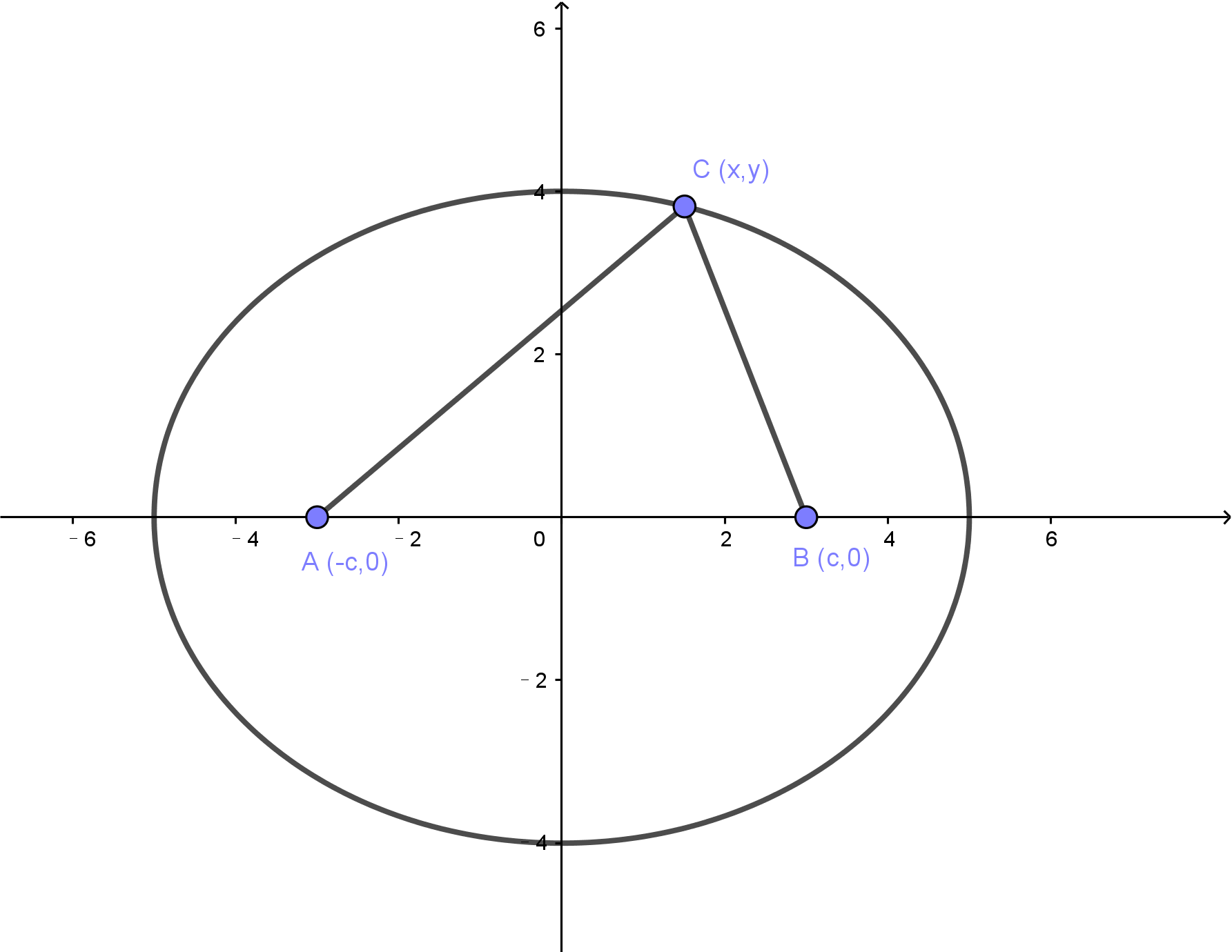
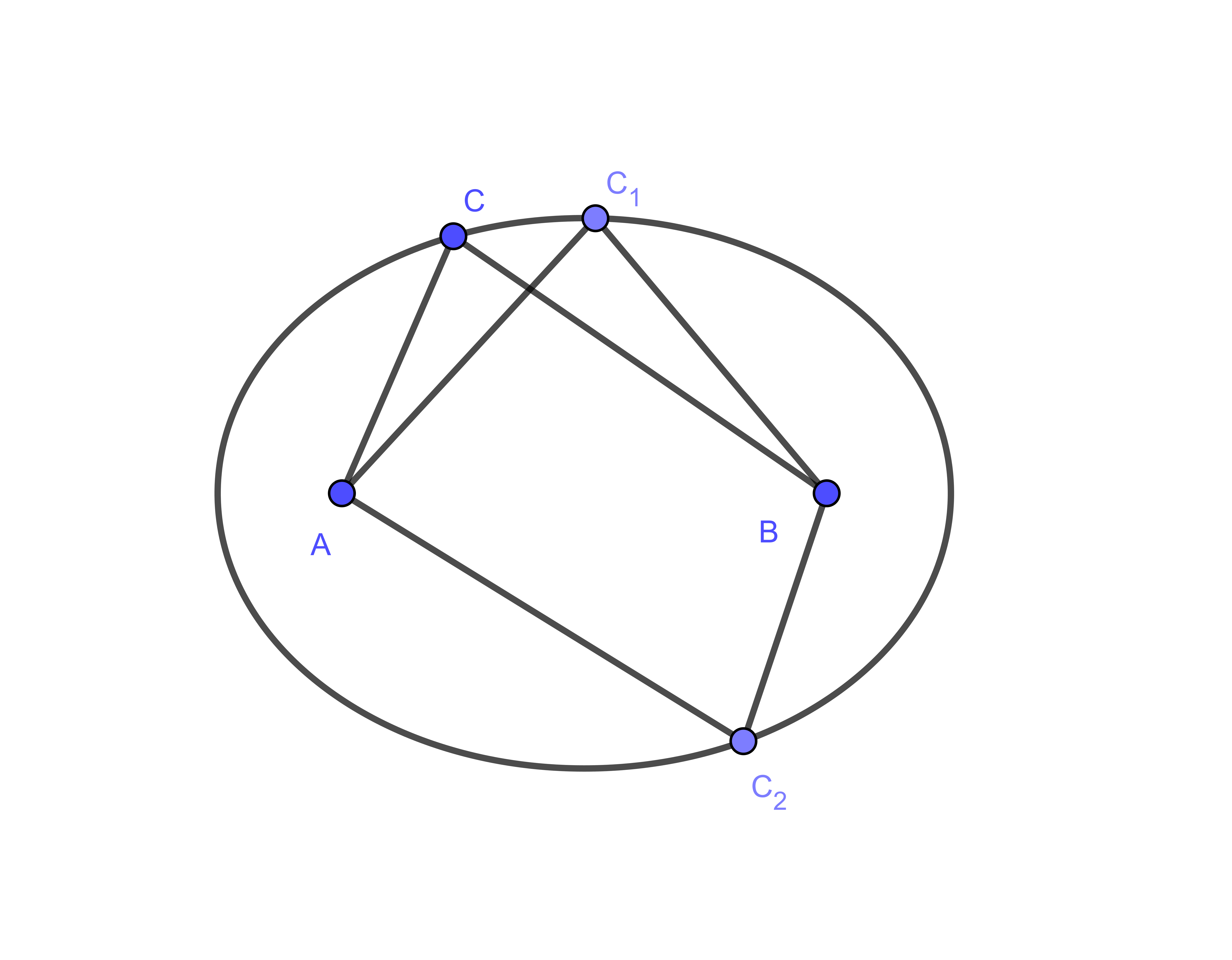
以x轴上两点A(-c, 0)、B(c, 0)作为焦点,求到两个焦点的距离为2a的椭圆方程。
假设椭圆上任意一点的坐标为C(x, y), 那么
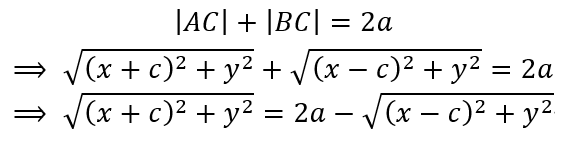
两边平方并化简
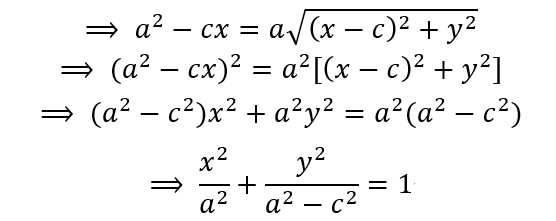
根据椭圆的定义,a>c,那么
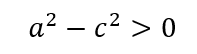
那么可假设
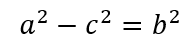
此时椭圆方程可化简为
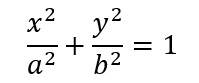
这就是焦点在x轴对称点上的椭圆标准方程。